【理科のコツ】てこの原理/かっ車と輪軸/ふりこ
読み時間目安：10〜15分
てこ・かっ車・ふりこ──「少ない力で動かす」しくみをまとめて理解しよう
このページでは、入試頻出のてこの原理・かっ車・ふりこを、
動画＋図解＋クイズで一気に整理します。
公式の丸暗記ではなく、「なぜそうなるのか？」までイメージでつかんでいきましょう。
このページで学べること
- てこの支点・力点・作用点と、少ない力で重いものを動かすコツ
- 定かっ車・動かっ車の役割と、クレーンなどへの応用
- ふりこの周期が「重さ」ではなく紐の長さで決まる理由
- 入試や定期テストでそのまま使える重要ポイント＋確認クイズ
1. てこの原理──支点・力点・作用点
てこは支点・力点・作用点の位置関係で「楽さ」が変わります。
同じ重さでも、支点から力点までの距離が長いほど小さい力で持ち上げられます。
「重い石をできるだけ楽に持ち上げたい」ときに活躍するのがてこです。
てこには次の3つのポイントがあります。
- 支点： てこ（棒）が回転する支えの点
- 力点： 手で力を加えている場所
- 作用点： 実際に物体（石など）が動いている場所
てこのキホンは、
「支点から力点までの距離が長いほど、必要な力は小さくなる」という点です。
実際に板や棒で試してみると、感覚的に理解しやすくなります。
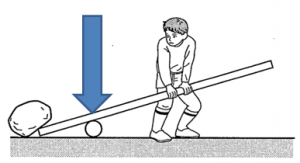
支点：てこを支えているポイント。
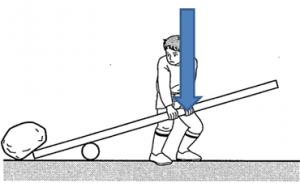
力点： 実際に手で力を加えている場所。
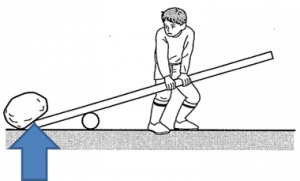
作用点： 力を受けて物体が動いている場所。
ハサミ・ペンチ・ピンセットなどの問題では、「どこを支えて」「どこに力を加えて」「どこが動いているか」を
イメージできると支点・力点・作用点を迷わず判断できます。
2. かっ車と輪軸──力の向きと大きさを変える道具
かっ車とは？
かっ車は、溝のついた車にロープ（ひも）をかけた道具で、
主に「力の向きを変える」ことや、「必要な力を小さくする」ことに使われます。
- 定かっ車： かっ車が固定されているタイプ。
力の向きを変えることができる（例：下向きに引いて上に持ち上げる）。 - 動かっ車： かっ車自体が荷物と一緒に動くタイプ。
2本のひもで1つの重さを支つため、必要な力が半分になる。
クレーン車などでは、動かっ車を何枚も組み合わせて、
とても重い荷物を「小さな力」で持ち上げるしくみが使われています。
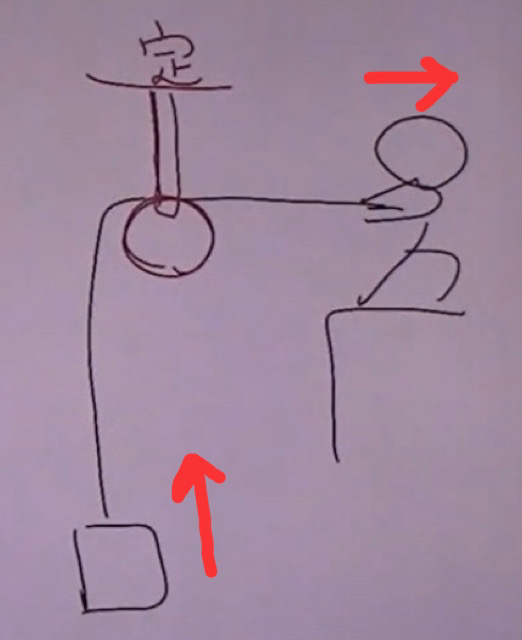
定かっ車は力の向きを変える、動かっ車は必要な力を小さくするのが役割です。
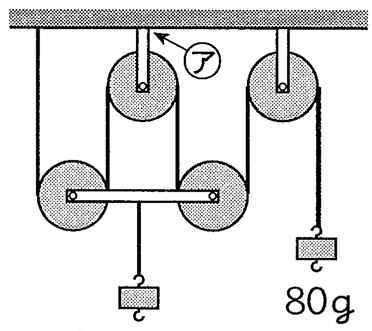
2本のひもで1つの重りを支えると、1本あたりの負担は半分になります。
4本で支えれば4分の1の力で持ち上げられます。
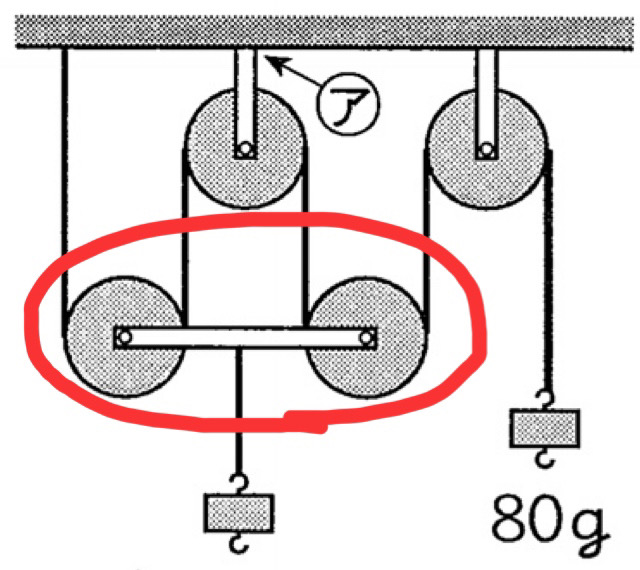
例えば、80 g のおもりとつり合っている動かっ車で、
4本のひもが重りを支えているなら、
- 1本あたりが支える重さ：80 g
- 合計で支えられる重さ：80 g × 4 = 320 g
クレーンでは動かっ車をたくさん重ねることで、1トンの荷物を1 kg 分の力で持ち上げるようなイメージになります。
「何本のひもが重さを支えているか？」を数えて、
必要な力 ＝ 全体の重さ ÷ ひもの本数 で考えるクセをつけよう。
3. ふりこ──周期は「重さ」ではなく「紐の長さ」で決まる
同じ場所でふりこを動かしたとき、周期を決めるのは紐の長さです。
重りの重さや振れ幅は、基本的には周期に関係しません。
ふりこ（ブランコのような動き）の1往復にかかる時間を周期と言います。
入試でよく狙われるポイントは、次の3点です。
- 周期は重さに関係しない。
- 周期は紐の長さで決まる。
- 紐が長いほど周期は長く、短いほど周期は短い。
実際の物理では、周期を
T = 2π√(ℓ / g) という式で表しますが、
g や π は一定なので、変化するのはℓ（紐の長さ）だけだと理解できればOKです。
「重い方がゆっくり動きそう」という直感と違うので、
「周期は紐の長さだけで決まる」という事実をしっかり覚えておこう。
まとめ
| ポイント | 内容 |
|---|---|
| てこの原理 |
・てこは支点・力点・作用点で構成される。 ・支点から力点までの距離が長いほど、少ない力で重い物を動かせる。 ・ハサミやペンチなどもてこの仲間。実験や体験を通して理解すると定着しやすい。 |
| かっ車 |
・定かっ車： 力の向きを変えるための装置（例：下向きに引いて物体を上げる）。 ・動かっ車： 2本以上のひもで重さを分担し、必要な力を小さくする。 ・クレーンなどで応用され、複数のかっ車を組み合わせてとても重い物を少ない力で持ち上げる。 |
| ふりこ |
・ふりこの周期は、吊るしている物体の重さに関係せず、紐の長さで決まる。 ・紐が長いほど周期は長く、紐が短いほど周期は短い。 ・ガリレオが発見したふりこの等時性が基礎となっており、入試の表・グラフ問題でもよく出題される。 |
てこ・かっ車・ふりこクイズ
学んだ内容をクイズで確認してみましょう。
「正解を見る」ボタンを押すと答えが表示され、ボタンは非表示になります。
| 問題 | 選択肢 | 回答 |
|---|---|---|
| 1. てこの支点とは何を指しますか？ |
A. 力を加える場所 B. 棒が回転する支えとなる点 C. 棒の両端 D. 作用が及ぶ場所 |
|
| 2. かっ車の主な役割は？ |
A. 力を増幅する B. 力の方向を変える C. 摩擦を減らす D. 温度を上げる |
|
| 3. 動かっ車を使うと力はどうなりますか？ |
A. 変わらない B. 倍になる C. 半分になる D. 1/4になる |
|
| 4. ふりこの周期を決める主な要因は？ |
A. 重さ B. 紐の長さ C. 振れ幅 D. 支点の位置 |
|
| 5. ガリレオが発見したふりこの特性は？ |
A. 重い物ほど周期が短い B. 周期は紐の長さで決まる C. 周期は振れ幅に依存する D. 周期は力の大きさで決まる |
|
| 6. クレーンで動かっ車が使われる主な理由は？ |
A. 重量を分散する B. 速度を上げる C. 摩擦を減らす D. 電力を節約する |
|
| 7. 動かっ車で4本の紐を使う場合、1本の紐と比べて持ち上げられる荷物の重さは？ |
A. 4倍 B. 半分 C. 同じ D. 1/4 |
|
| 8. ふりこの振れ幅が少し変わっても、周期に大きな影響はありますか？ |
A. はい、影響します B. いいえ、影響しません C. 部分的に影響します D. 温度に依存します |
|
| 9. 支点が作用点に近いと、物を動かすために必要な力はどうなりますか？ |
A. 増える B. 減る C. 変わらない D. 方向が変わる |
|
| 10. 紐が長いふりこの周期はどうなりますか？ |
A. 短い B. 長い C. 同じ D. 不定 |
|
さいごに：公式よりも「イメージ」を優先しよう
てこ・かっ車・ふりこは、どれも「少ない力でうまく動かす」ための道具・現象です。
公式を覚えることも大切ですが、まずは
「どう動いているのか」「なぜその方が楽なのか」をイメージでつかむことが、得点アップの近道になります。
- 自分で簡単な模型（てこ・かっ車・ふりこ）を作って、実際に動かしてみる
- 教科書の実験結果の表・グラフを言葉で説明できるか確認する
- 理科と算数（比例・反比例など）をセットで考えるクセをつける
「イメージで分かる」と、応用問題や文章量の多い入試問題でも怖くなくなります。
受験理科専門塾 しゅん吉クエスト
物理分野を武器にしたい受験生へ
「公式は覚えたけれど、なぜそうなるのかが分からない…」
「文章問題になると急に解けなくなる…」という悩みを、
しゅん吉クエストの物理攻略講座で一緒に解決しませんか。
てこ・かっ車・ふりこ以外にも、力学・電気・光・音をまとめて整理していきます。
