【理科のコツ】てこの原理/かっ車と輪軸/ふりこ

てこの原理

今回は、てこの原理について見ていきましょう。
さて、石を持ちあげるのに一番楽だと想像出来るのはどれでしょうか？図1、図2、図3のどれが良さそうだと思いますか？

なくとなくやった事があるというのは、大きいです。実際に実験や体験する事が凄く大事です。
一生懸命机に向かって勉強するだけじゃなく色んな事を体験するというのは凄く大事になります。
実際これをグイっとしたら石がゴロンってなるだけで、なんの為にこんな事をしているのか？
問題文にちょっとツッコミを入れながら感情移入をして問題を解いてみると、条件の読解がしやすくなると思います。

てこの原理を初めて聞くという人もいるかもしれません。順番的に支点・力点・作用点というポイントがありますが
今はそこの名前まで覚えなくていいです。一番軽い力でお得に仕事が出来るのはどれ？という問題です。

重いものを持ち上げたいな、と思う事が皆もあると思います(あるのかな。。。(笑))
そんな時にどうしたらいいかというとこのように支える棒を準備します。この支え方も棒をもっと長くしていけばダメではないです。グワっと長くしてけば、別にいいです。こんな尖っていたらバキっと折れそうな感じもします。

ここで棒が支えられているというのは分かりますか？さっき言ったように、ここで折れそうな感じがするな
という感覚を持つ事も大事です。
こうやって支えているポイントの事を支点と言います。

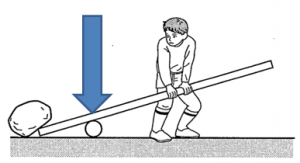
ではどこに力を加えているかというと、こういう力を加えている所を、力点と言います。

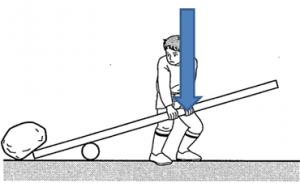
この部分が、仕事として作用してくるので作用点と言ったりします。

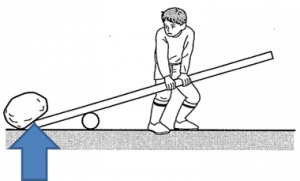
目線を変えると、力点や作用点という場所が変わったりします。
なので、ハサミやピンセットなどの問題として「どこが支点・力点・作用点でしょう？」という問題が出たりします。ただ暗記するという事ではなく、ここに力加えているな、その結果ここで作用しているな、という意味合いを理解していくという事が大事になってきます。
実はこの支点から距離が長い方がもの凄いお得にこちら側をクルンと回転させる事が出来ます。
実際に自分たちでこのような実験とかをしてみて緩い力で石ころを転がせるか？というのを体験してみると
こういった問題がスムーズに解けるようになります。
一緒に勉強していきましょう。

かっ車と輪軸

今回は、かっ車と輪軸について喋っていきます。

かっ車は、そもそもなんの為にあるかご存知ですか？
そもそもかっ車が何物を知らないで、「動かっ車と定かっ車の二種類あり、定かっ車だったらこうで動かっ車だったらこう」と暗記している生徒はいっぱいいます。
もちろん暗記して覚える事も大事なんですが、そもそもかっ車がなんの為に生まれたのかというと、
「力の向きを変える為」です。なにが？ってなると思いますが(笑)

例えば、右に物をドンッと押したら、普通は物は右に行くと思います。
右に物をドンッって押したのに、左に行ったらかっこよくないですか？(^^)
それが、かっ車で出来ます。

例えばこれは、固定して動かないから定かっ車と言います。
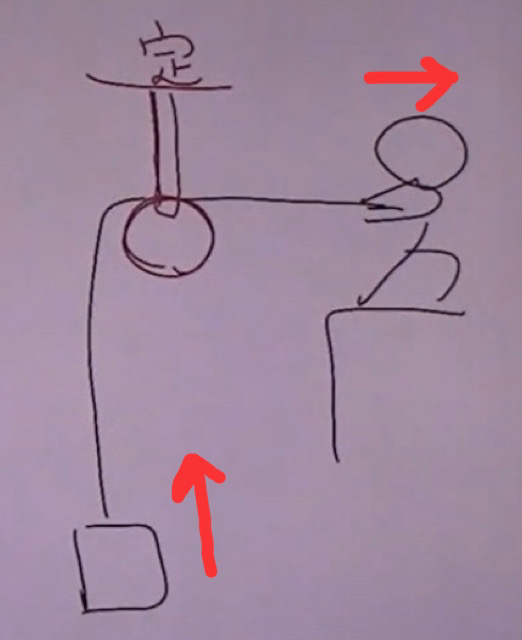
そこに紐をヒュンヒュンと吊るします。こっちは崖の上に登っておきます。そして、ここに荷物があります。この人は、エイッってこっちに力を引っ張ります。

なのに、物体はエイッて上に動きます。凄くないですか？(笑)
こっちに引っ張ったのに上に浮くんです。なぜ？って思いませんか？
素晴らしい発明です。凄いですよね(^^)
このように、力を加えた向きとは違う方向に作用させる事が出来るという技です。

では、動かっ車がなんの為にあるんですか？
そもそも動かっ車を知っていますか？そう、動くかっ車です。
どんな所で利用されているか聞いた事がありますか？
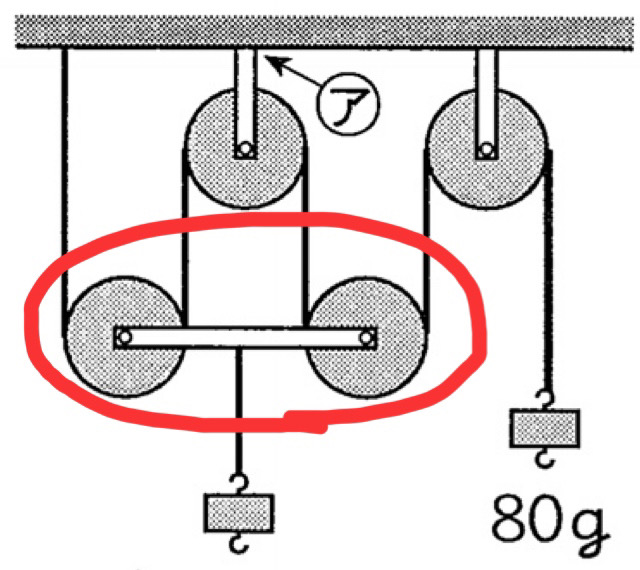
動かっ車は、この図だとこちらになります。

おもりの部分の紐を引っ張ると、これがシャーシャーって動きます。想像出来ますか？
これがなんなのかというと、ウィンって引っ張ると物体はウィンって上に浮きますが、これは2本の紐で吊るしています。
例えば、これは10kg分の重さなんですが、5kg分と5kg分ですみます。凄い便利です。
一人で袋の荷物持つより、友達と一緒に持った方が力は半減で済みます。だから2本の紐で吊っているので、力は半分になるという特徴があります。これは聞いた事ある人も多いと思います。

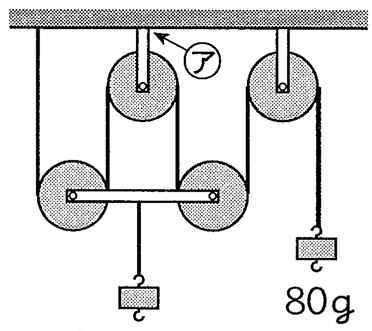
先生、私はこういう複雑な問題を解きたいんだよ、と言う方もいると思います。でも、これも簡単な問題です。
80ｇのおもりとちょうど吊り合っています。そして、このおもりAは4本の紐で吊っています。だから、実は80×4＝320ｇまで吊るす事が出来ます。本当に？重いからこちら側に落ちるんじゃない？と思うかもしれないですが、80ｇずつ力が付加されて支え合っているので、こんな感じで解く事が出来たりします。

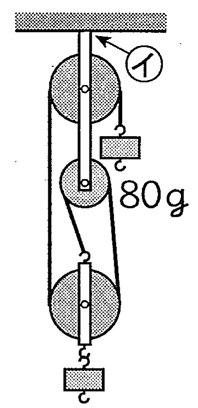
こちらの問題はどうやって解くのかいうと、これは3本で吊っています。
だから80グラム分の力がここに掛かるので、80、80、80という事で240になります。

実はこの動かっ車は日常生活だとビル建築しているクレーンで使われています。
こんなクレーン車が凄い重い物を吊るしていないですか？

これを見て、あーって崩れ落ちそうなのを想像した事ないですか？
あんな重い物持って大丈夫かよ、と思うかもしれませんが、実はここのクレーンの所にこういったフックが引っ掛かっていて、ここに実は動かっ車が10枚20枚ぐらい付いています。
さっき1枚で力は半減すると言いました。だから、2枚だと4分の1、3枚で8分の1、10枚だと1024分の1になります。
すなわち、1000分の1ぐらいの力で吊るせます。だから1トンという重い物体も、1キロ分で引っ張る事が出来ます。
凄いでしょ？

このように、理科で使われる道具がなんの為に使われてどういった所で利用されているのかというのを理解すると、意外とこういった問題もスムーズに解けるようになっていきます。
という事で、一緒に学習していきましょう。

ふりこ

今回は、ふりこについて喋っていきます。
ふりこは見た事ありますか？
催眠術師の人がやっていますよね。最近は知らないですかね？(笑)
ふりこを見て寝る人あんまりいないですからね。
つまらない授業を聞いた方が眠くなりますよね。
ふりこは公園とかだとブランコみたいなもので、シンプルにこんな感じです。
振れ幅ですが、こっちの方が振れ幅が大きくなるような事はないですよね？
ブランコやっていて、真ん中よりこっちだけ揺れてこっちはあんまり揺れなくて、こっちだけ揺れてこっちだけ揺れないのはおかしいですよね。
だからこれはどのジャンルでも言えますが、物理は実験したり体験すると現象として凄く理解出来ます。
なので、まず皆はブランコに乗る所から始めてみましょう。
そうすれば、ふりこをマスター出来ます。
この間違った図は一回消します。
例えば、こんな問題とか色々出てきます。
特にふりこは、周期と絡めていきます。
周期とはなにか？と思いますよね？
敢えて漢字で書きます。
小学校1、2年生の子はパパとママに聞いてみて下さい。
これは周期と言います。
しゅん吉ではないです。
しゅん吉は私の名前です。
この周期は、実は重さは関係ないんです。
紐の長さのみで決まってきます。
例えばこの問題だと、Cが50グラムでBが20グラムです。
重い方がスピードが遅くてあまり揺れないのではないかと思いますか？
20グラムと20グラムだったら同じタイミングで返ってくるのではないかと思いますか？
微妙に直感に反する所が出てきます。
実際は空気抵抗とかもあります。
さっきはブランコと言いましたが、ブランコとかの場合は自分で漕いで勢いをつけたりするので、こういう問題とは経験する現象がちょっと異なります。
なので、自分たちが想像しているものと現実の数式で証明されている実際のものにズレがある問題というのはめちゃくちゃ受験には狙われてきます。
それの代表例です。
今ふりこはグラム数は関係ないと言いました。
シンプルに、紐の長さだけで戻ってくるタイミングの周期、時間というのが決まっています。
見て下さい。
私の右手と左手の長さは一緒です。
その時に振れ幅ですが、例えばこれは振れ幅50度60度とかズラしています。
例えばこっちの振れ幅はこれぐらいです。
こっちの振れ幅これぐらいです。
そうしたらどっちの方が時間が掛かると思いますか？
こっちの方が短いから早いと思いますか？
いきます。
よーい、どん。
1、2、3、うまくないですか？
4、5、お前のさじ加減じゃないのかと思うかもしれないですが、これはマジです。
分かりますか？
ここから1で帰ってくるのと、1で帰ってくるのが一緒なんです。
紐の長さで決まります。
だからちょっとズレていて、なんか左の方が早く帰ってくるな、となった場合は左の手がちょっと短いという事です。
言っている事が分かりますか？
そう、短ければ短いほど、早く帰ってきます。
長ければ長いほど、いーちって帰ってきます。
この周期というのが紐の長さによって決まるから、吊るしている物体とかどうでもいいんです。
こういうのがよく問題に狙われてきます。
表とか使ったような問題になってきます。
実際周期はタイムだからTという記号を使うんですが、公式は2π√ｌ/ｇとなります。
ｌは紐の長さです。
凄く簡単な数式ですよね。
こういうのをうちの塾ではバンバン教えていきます。
もちろんこんな難しい話はしません。
実はこの数式を俺が考えたち言いたいんですが、ガリレオというおっちゃんがいるの知っていますか？
タレントの福山雅治さんではないです。
ガリレオという昔にいた凄い賢い人が、ふりこの等時性を発見しました。
これを見て分かるようにグラム数で、ｇは地球上では9.8という数字です。
πは3.14です。
円周率は習いましたか？
まだ習ってないですか？
これらは決まった数字なので、lしか数字が変わるものがないんです。
だから、実は周期は紐の長さによって決まるんです。
実際この√という記号を小学生に解かせる事はもちろんしません。
そういうのが実験の表のデータとして入っていきます。
なので、そういったデータからうまく読み取って問題を解いてくという所に発展していきます。
なので、色んなパターンの問題があるので一緒に勉強していきましょう。